Формування математичних компетентностей випускника загальноосвітньої школи та система роботи з обдарованою учнівською молоддю в умовах сільської школи
Формування компетентностей учнів зумовлене не тільки реалізацією відповідного оновленого змісту освіти, але й адекватних методів та технологій навчання. Продуктивне навчання забезпечує засвоєння знань та умінь, володіючи якими випускник школи знаходить підґрунтя для свого подальшого життя.
Продуктом школи є людина, особистість, тому підлягають реалізації такі задачі:
• створення умов для розвитку та самореалізації учнів;
• задоволення запитів та потреб школяра;
• засвоєння продуктивних знань, умінь;
• розвиток потреби поповнювати знання протягом усього життя;
• виховання для життя в цивілізованому громадянському суспільстві.
Математична освіта покликана зробити вагомий внесок у формування ключових компетентностей учнів як загальних цінностей, що базуються на знаннях, досвіді, здібностях, набутих завдяки навчанню. Отримані у школі знання та сформовані вміння і навички є, безперечно, важливими, але нині особливої актуальності набуває компетентність учня в різних галузях знань. Саме компетентності більшість міжнародних експертів вважають тими індикаторами, що дають змогу визначити готовність учня- випускника до життя, подальшого особистого розвитку та активної участі в суспільному житті.
З точки зору компетентнісно зорієнтованого підходу до організації навчально-виховного процесу, зміст математичної освіти спрямований на досягнення таких цілей:
• інтелектуальний розвиток учнів, формування видів мислення;
• оволодіння прийомами математичної діяльності, які необхідні у вивченні суміжних предметів;
• формування уявлень про математику як форму опису і метод пізнання дійсності;
• виховання учнів у процесі навчання математики;
• формування позитивного ставлення та інтересу до математики.
За визначенням С. А. Ракова, математична компетентність — це спроможність особистості бачити та застосовувати математику в реальному житті, розуміти зміст і метод математичного моделювання, будувати математичну модель, досліджувати її методами математики, інтерпретувати отримані результати, оцінювати похибку обчислень.
Для успішної участі у сучасному суспільному житті особистість повинна володіти певними прийомами математичної діяльності і навичками їх застосувань до розв’язування практичних задач. Значні вимоги до шкільної математичної освіти у розв’язанні практичних задач ставлять сучасний ринок праці, отримання якісної професійної освіти, продовження освіти на наступних етапах. Тому одним із головних моїх завдань навчання математики є формування в кожного учня математичної компетентності.
Отже, в своїй педагогічній діяльності ставлю за мету використання напрямів набуття математичної компетентності учнів:
*Будувати і досліджувати найпростіші математичні моделі реальних об’єктів, процесів і явищ.
*Володіти необхідною оперативною інформацією для розуміння постановки математичної задачі.
*Володіти технікою обчислень.
*Уміти проектувати і здійснювати алгоритмічну та евристичну діяльність на математичному матеріалі.
*Уміти працювати з формулами.
*Уміти будувати і читати графіки функціональних залежностей, досліджувати їхні властивості.
*Уміти класифікувати і конструювати геометричні фігури на площині і у просторі.
*Уміти оцінювати шанси настання тих чи інших подій, міру ризику під час того чи іншого рішення, обирати оптимальний варіант.
Адже математична компетентність є важливим показником якості математичної освіти, природничої підготовки молоді.
Компетентність випускника загальноосвітньої школи ставлю як завдання і як місію освіти, і ця компетентність повинна забезпечити йому, з одного боку, можливість самореалізації у суспільстві, а з другого боку – сприяти розвитку гуманізму, демократії у самому суспільстві, становленню та поглибленню громадянського суспільства.
Кожен з учнів через певний проміжок часу стає перед вибором свого життєвого шляху. А математика – це наука, яка формує людину, очищує її розум, а відповідно, її душу, формує повагу до істини.
Наш час висуває нові завдання перед наукою і практикою, стимулює розвиток нових навчальних технологій, оригінальних виховних ідей, форм і методів навчання та виховання.
Я більше тридцяти років працюю в сільській школі, в якій немає паралельних класів, а кількість дітей з року в рік поступово зменшується, що призводить до зменшення навантаження вчителів додатковими годинами та факультативними курсами. А про класи з поглибленим вивченням математики нам залишається тільки мріяти.
Спілкуючись з випускниками школи, які навчаються у вищих навчальних закладах, я усвідомила, що наші випускники не поступаються своїми інтелектуальними і соціальними здібностями випускникам міських навчальних закладів. Підтвердженням цього є те, що наші випускники після закінчення вузів посідають керівні посади та здобувають великі успіхи на своєму трудовому шляху.
У процесі викладання математики особливу увагу приділяю роботі з обдарованими дітьми. Важливою умовою розвитку обдарованої дитини для мене є її інтелектуальні та психологічні особливості. Кожна обдарована дитина – індивідуальність, яка потребує особливого підходу. У своїй практичній діяльності використовую такі методи навчання:
• Метод конкретної ситуації (вчу школярів думати, узагальнювати, аналізувати, розглядати різні варіанти, складати свої задачі).
• Метод інциденту (учні вчаться долати інертність, переборювати стресові ситуації, що так важливо у житті).
• Метод мозкового штурму (привчаю учнів на поставлені запитання давати свої варіанти відповідей).
• Метод занурення (створюю ситуації, де учні з головою занурюються в поставлені завдання, ефективно розв’язують їх).
• Метод евристичних питань (спонукаю учнів думати, аналізувати).
• Кооперативний метод (використовую при роботі в групах).
• Дослідницький метод.
• Метод проектів.
Застосовуючи метод проектів, стимулюю учнів до розв’язання проблем; розвиваю критичне мислення; учні набувають навичок роботи з інформацією; вчаться вирішувати пізнавальні, творчі завдання у співробітництві.
Досягнення максимально можливого рівня забезпечую шляхом регулярної перевірки розуміння змісту підручника, що привчає учнів до самостійної роботи з книгою. З цією метою використовую математичні диктанти, що перевіряються самими ж учнями. Така форма проведення математичного диктанту дозволяє навчити їх об᾽єктивно оцінювати свої знання і виправляти власні помилки відразу після виконання роботи. Гарні результати дає проведення диктантів із взаємоперевіркою, наприклад, сусіда по парті.
Залучаючи дітей у групи,враховую їх індивідуальні можливості. А тому завдання для учнів стараюся підбирати індивідуальні, а для роботи в групах – різнорівневі.
На своїх уроках широко використовую інтерактивні засоби навчання, добиваючись того, що в учнів зростає зацікавленість математикою, рівень знань учнів підвищується.
В своїй роботі з учнями, які проявляють інтерес до вивчення математики і мають високий рівень знань, використовую такі форми роботи:
• розв᾽язування цікавих і складних задач;
• самостійне вивчення окремих тем;
• написання рефератів;
• допомога вчителю на уроках («учні – консультанти», «учні – вчителі»);
• участь в реалізації плану позакласної роботи з математики (тиждень математики, олімпіада, інтелектуальні конкурси, математичні ігри, тощо);
• складання та розв'язування учнями тестів , задач , кросвордів тощо. ●участь у міжнародному конкурсі «Кенгуру».
В цьому навчальному році 10 моїх учнів взяли участь у міжнародному конкурсі «Кенгуру» і вибороли: 4 сертифікати відмінних результатів, 6 – добрих.
При підготовці учнів до ЗНО з математики керуюся такими методичними рекомендаціями як актуалізація знань з вивченого матеріалу, ознайомлення учнів з програмовими вимогами ЗНО, демонстрування випускникам усіх форм тестових завдань, проведення домашніх, самостійних та контрольних робіт із використанням тестів.
Ознайомлюю учнів з алгоритмами виконання тестових завдань різних форм. Привчаю учнів виконувати завдання не лише правильно, але й швидко, щоб максимально наблизити їх до умов, у яких випускники працюватимуть під час зовнішнього оцінювання.
На уроках узагальнення та систематизації навчального матеріалу намагаюся системно й ефективно повторити курс математики загальноосвітньої школи, виявити прогалини у знаннях того чи іншого матеріалу, сформувати сталі навички застосовувати знання як під час виконання традиційних завдань, так і під час розв᾽язування задач підвищеної складності.
Підбираю учням завдання різної форми: з вибором однієї правильної відповіді, з короткою відповіддю, з повним обґрунтуванням. Деякі тести містять завдання на встановлення відповідності. Тобто, стараюся приблизити учнів до умов складання ЗНО. Підбираю тестові завдання,що структуровані за змістовими лініями: числа та обчислення, вирази та їх перетворення, рівняння та нерівності, функції, ймовірність і статистика, геометричні фігури та їхні властивості.
Така запропонована учням мною методика дає позитивні результати. Так в цьому році з десяти випускників моєї школи сім учнів здавали незалежне оцінювання з математики, що становить 70% загальної кількості випускників. Результати, отримані учнями такі: чотири учні набрали від 170 до 196балів, три учні – від 140 до 170балів.
Маючи факультатив у 11 класі, використовую його як допоміжний засіб підготовки учнів до здачі незалежного оцінювання, а деякі його теми стають у пригоді учням, які беруть активну участь в олімпіадах Ι – ΙΙΙ етапів. В цьому навчальному році у випускних класах проводила факультативи з тем: «Методи розв᾽язування задач з математики» та «Розв᾽язування задач із параметрами». Проведення факультативних занять у школі сприяє досягненню таких цілей як підвищення рівня математичної підготовки, реалізації навчання методам і способам розв᾽язування задач, інтелектуального розвитку учнів, розвитку їх логічного мислення,інтуїції.
Готуючись кожний раз до проведення факультатива, ставлю перед собою завдання: як найглибше розвинути потенціальні творчі здібності кожного обдарованого учня.
Але як тільки настає новий навчальний рік, то зразу виникає питання, чи виділиться з варіативної частини година на факультативний курс, адже із інших предметів теж потребують цієї години, а програма в сільських школах з кожним роком зменшується. Чому ж тоді обдаровану дитину з села потрібно ставити в такі «рамки», чим вона гірша від міських дітей, в яких у школах є класи з поглибленим вивченням математики? Адже зовнішнє тестування, обласну олімпіаду вони пишуть разом. І, напевно, ця дилема залишиться ще довго не розв᾽язаною. Додаткові заняття з математики мені, як і кожному сільському учителю, доводиться проводити за рахунок свого власного часу.
Готуючи учнів до участі в олімпіаді, ефективною формою позакласних занять з математики є гурток, де разом з учнями розв᾽язуємо нестандартні задачі, тобто задачі, умови яких сформульовано так, що вони не належать до жодного з типів з шкільного курсу математики. Як правило, кожна з таких задач потребує логічного мислення, просторової уяви, кмітливості та особливого підходу при її розв᾽язуванні, знаходження якого вимагає від учня інтенсивної розумової праці.
Геніальний Ісаак Ньютон стверджував: «Для вивчення наук задачі корисніші за правила». Саме з розв᾽язування задач розпочинається шлях у науку.
Я можу пишатися своїми учнями, зокрема Кислим В᾽ячеславом,учнем 11 класу, який в минулому році на Всеукраїнській олімпіаді ΙΙΙ етапу виборов ΙV місце, а в цьому році отримав диплом ΙΙΙ ступеня. Дипломом ΙΙΙ ступеня нагороджена і учениця 9 класу Кисла Ольга.
Пропрацювавши понад 30 років на педагогічній ниві, я зрозуміла, що життя – це великий глобальний проект, у якому тісно пов᾽язано й минуле, й сучасне, й майбутнє. І складається воно з наших, здавалося б, маленьких проектів. Головними проектами в моєму житті є мої діти, мої учні. І завдання моє перед ними — розвиток їх здібностей і навичок, підвищення престижу знань, формування математичних компетентностей, вміле використання випускниками школи набутих у процесі навчання вмінь і практичних навичок у повсякденному житті.
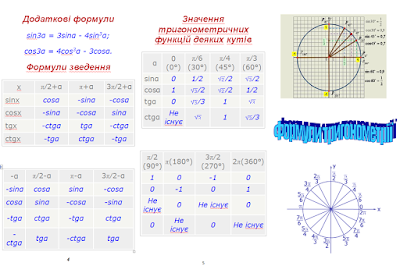
Тригонометричний буклет
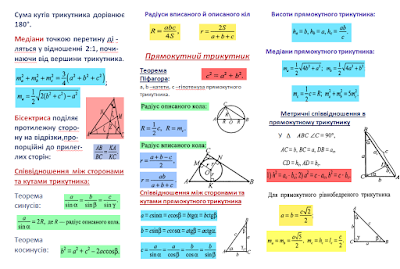
Буклет з геометрії "Трикутники"









Немає коментарів:
Дописати коментар